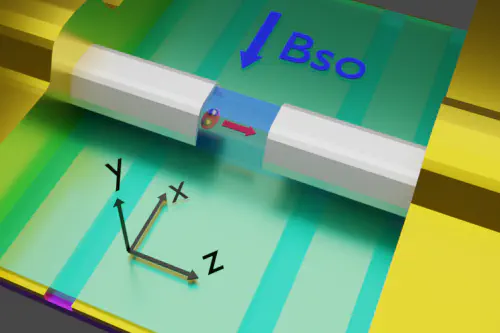
 A Cooper pair transits through a nanowire. picture Bomin Zhang
A Cooper pair transits through a nanowire. picture Bomin ZhangA Josephson junction is a superconducting electronic device consisting of two superconducting electrodes separated by a thin insulating barrier. Current can flow through this junction without any resistance and is called the supercurrent. Supercurrent is caused by Cooper pair tunneling, where pairs of electrons (Cooper pairs) can tunnel through the insulating barrier and flow between the two superconducting electrodes.
The current-phase relation (CPR) in a Josephson junction describes the relationship between the supercurrent flowing through the junction and the phase difference between the superconducting wave functions on the two sides of the junction. The CPR for a normal Josephson junction is given by:
We observe skewed critical current patterns with an external magnetic field, i.e.,